Поскольку этот учебник относится к разработке игр, он представляет собой краткое и практическое введение в линейную алгебру. Линейная алгебра - это изучение векторов и их использование. Векторы имеют много направлений в применении как в 2D, так и в 3D-разработке, и Godot широко их использует. Хорошее понимание линейной алгебры имеет важное значение для того, чтобы стать сильным разработчиком игр.

Этот учебник не является формальным учебником по линейной алгебре. Мы будем рассматривать только то, как она применяется в разработке игр. Для более широкого изучения линейной алгебры в разработке игр я советую ознакомиться со следующей статьей см. click (ru).

Системы координат (2D)

В 2D пространстве координаты определяются с использованием горизонтальной оси (x) и вертикальной оси (y). Отдельная позиция в 2D-пространстве записывается как пара значений - (4, 3).

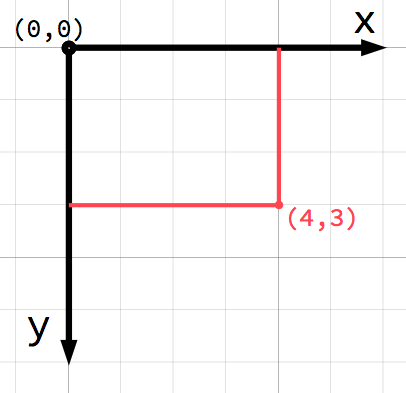
Если вы новичок в компьютерной графике, то вам могло показаться странным, что положительная ось (y) показывает вниз, а не вверх, как вы, вероятно, изучали в учебном заведении. Однако такой подход распространен в большинстве приложений для компьютерной графики.

Таким образом любая позиция в 2D-плоскости может быть обозначена парой чисел. Однако мы можем представить точку (4, 3) как смещенную точку от (0, 0) или от начала координат. Нарисуйте стрелку, от начала координат до точки (4, 3) указывающую направление:

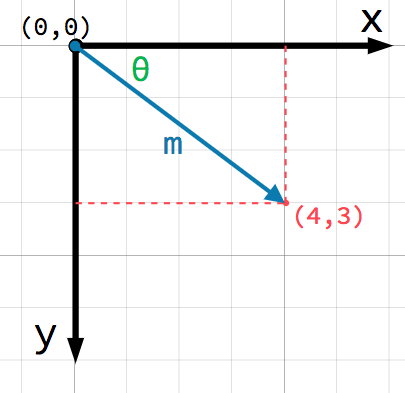
Это вектор. Вектор дает много полезной информации. Мы можем сказать, что точка находится в (4, 3), также можем рассматривать ее как угол θ и длину (некую величину) m. В этом случае стрелка представляет собой вектор положения - она обозначает положение в пространстве относительно начала координат. Важным моментом для рассмотрения векторов является то, что они представляют только относительное направление и длину. Нет понятия конкретного положения вектора. Следующие два вектора идентичны (коллинеарные векторы):

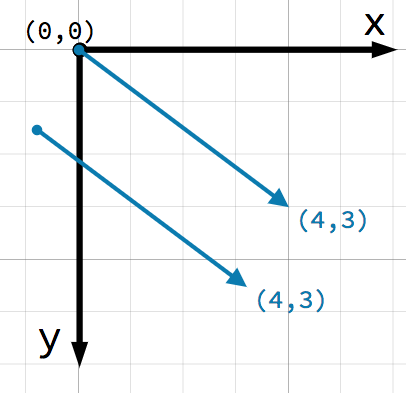
Оба вектора представляют точку, смещенную на 4 единицы вправо и 3 единицы вниз, относительно некоторой начальной точки. Неважно, где на плоскости вы рисуете вектор, он всегда представляет относительное направление и длину.

Операции над векторами

Вы можете использовать любой метод (координаты x и y, угол или длину) для обозначения вектора, но для удобства программисты обычно используют обозначение координат. Например, в Godot начало координат - верхний левый угол экрана, поэтому для размещения 2D-узла с именем Node2D (400 px вправо и 300 px вниз) используйте следующий код:

$Node2D.position = Vector2 (400, 300)

Godot поддерживает как Vector2, так и Vector3 для использования в 2D и 3D пространстве соответственно. Математические правила, которые обсуждаются в этой статье, применимы к обоим типам.

Поля вектора

Значение полей вектора можно получить через его переменные.

# создаем вектор с координатами 2 и 5
var a = Vector2(2, 5)
# создаем вектор и назначаем вручную значения x и у
var b = Vector2()
b.x = 3
b.y = 1

Сложение векторов

При добавлении или вычитании двух векторов добавляются или вычитаются соответствующие поля:

var c = a + b  # (2, 5) + (3, 1) = (5, 6)

Визуально это выглядит примерно так: добавляется второй вектор в конец первого:

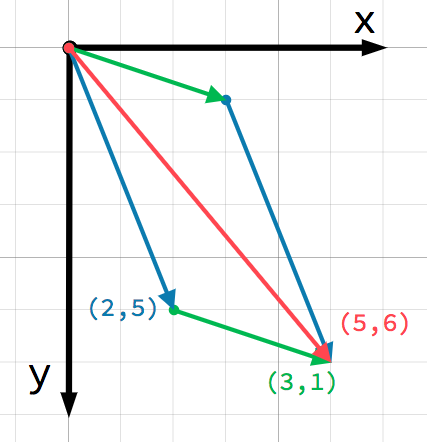
Обратите внимание, что сложение a + b дает тот же результат, что и b + a.

• Умножение вектора на число

Когда мы говорим о векторах, мы называем отдельные числа скалярами. Например, (2, 5) — вектор, а 2 — это скаляр.

Вектор можно умножить на число (скаляр):

var c = a * 2  # (2, 5) * 2 = (4, 10)
var d = b / 3  # (3, 6) / 3 = (1, 2)

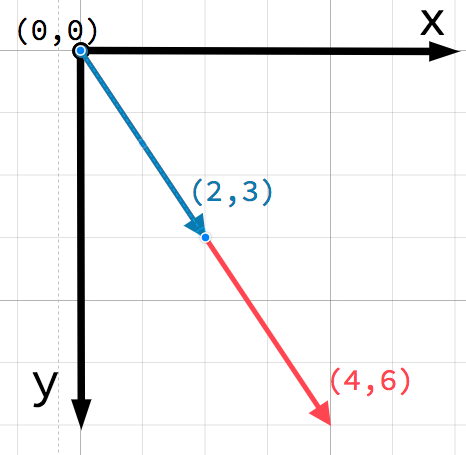
Умножение вектора на скаляр никак не изменит его направление, изменит только его длину. Вы как будто масштабируете вектор.

Практическое применение

Давайте рассмотрим два общих примера для сложения и вычитания векторов.

• Движение

Вектор может представлять любую величину с длиной и направлением. Типичными примерами являются: положение, скорость, ускорение и сила. На изображении ниже космический корабль на шаге 1 имеет вектор положения (1,3) и вектор скорости (2,1). Вектор скорости показывает, как далеко переместится судно на следующем шаге. Мы можем найти положение для шага 2, добавив скорость в текущее положение (1,3).

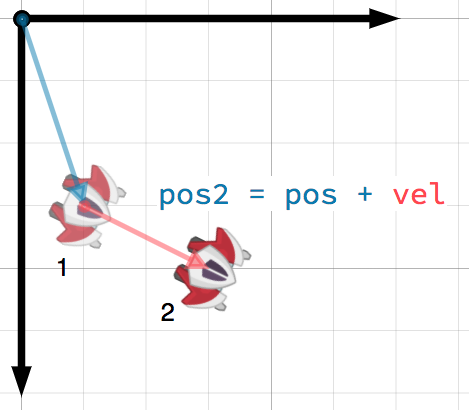
Скорость описывает изменение положения объекта за единицу времени. Новое положение можно найти, добавив скорость в предыдущую позицию.

• Направление на цель

В этом случае у вас есть танк, который хочет направить свою башню на робота. Вычитая положение танка из положения робота, вектор укажет направление от танка к роботу.

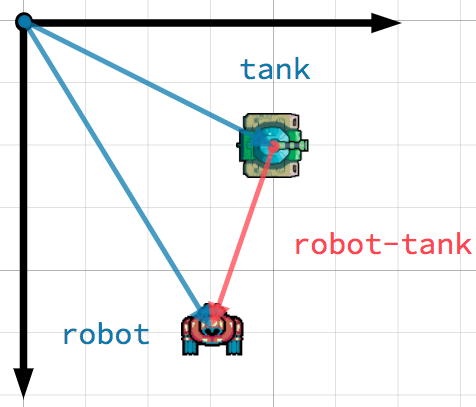
Чтобы найти вектор, указывающий А на В используйте В – А.

Единичные векторы

Вектор с длиной равной единице называют единичным вектором. Его также принято называть нормализованным вектором. Единичные векторы полезны тогда, когда вы имеете дело с направлением.

Нормализованный вектор

Нормализованный вектор получают путем уменьшения его длины до единицы с сохранением его направления. Это делается путем деления каждого из его компонентов на некую длину:

var a = Vector2(2, 4)
var m = sqrt(a.x*a.x + a.y*a.y)  # находим значение m с помощью теоремы Пифагора
a.x /= m
a.y /= m

Существует общий способ, который обеспечивает операцию «нормализации» для Vector2D и Vector3D:

a = a.normalized()

Поскольку нормализация включает деление на длину вектора, вы не можете нормализовать вектор длиной равной 0. Попытка сделать это приведет к ошибке.

Отражение

Обычно единичные векторы используют для обозначения нормалей. Нормальный вектор прямой - это единичный вектор, направленный перпендикулярно к поверхности, определяющий ее направление. Они обычно используются для освещения, столкновений и других операций, связанных с поверхностями.

Например, представьте, что у нас есть движущийся мяч, который бы отскакивал от стены или другого объекта:

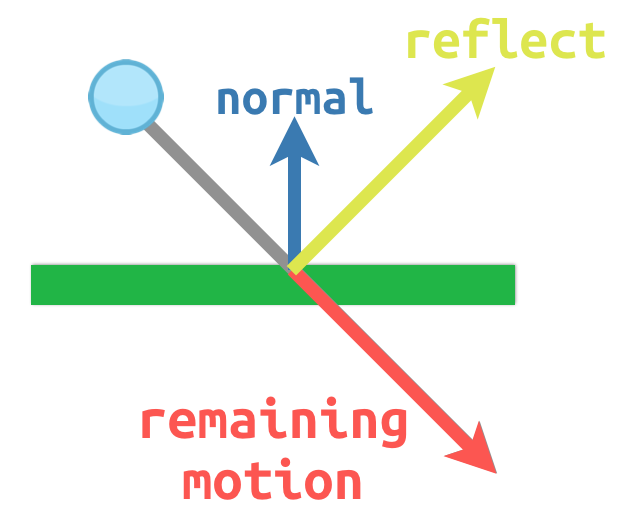
Нормаль поверхности имеет значение (0, -1), потому что это горизонтальная поверхность. Когда шар сталкивается c поверхностью, мы берем его оставшееся движение (значение, когда он касается поверхности) и отражаем его с помощью нормали. В Godot класс Vector2 имеет метод bounce() для обработки этого. Ниже пример на GDScript, диаграммы представленной выше, используя KinematicBody2D:

# содержание информации объекта о столкновении
var collision = move_and_collide(velocity * delta)
if collision:
    var reflect = collision.remainder.bounce(collision.normal)
    velocity = velocity.bounce(collision.normal)
    move_and_collide(reflect)

Скалярное произведение (Dot product)

Скалярное произведение - это операция двух векторов, результатом которой является скаляр (произведение величин этих векторов, умноженное на косинус угла между ними). Скаляр является одним из наиболее важных понятий в линейной алгебре, но часто понимается неправильно. В отличие от вектора, который содержит длину и направление, скалярное значение содержит только длину.

Формула скалярного произведения имеет две общие формы:

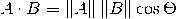
а также:

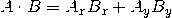
Однако в большинстве случаев проще всего использовать встроенный метод. Заметим, что порядок двух векторов не имеет значения:

var c = a.dot(b)
var d = b.dot(a)  # они эквиваленты

Скаляр наиболее полезен при использовании единичных векторов, из первой формулы видно, что все сводится к нахождению cos(). Это означает, что мы можем использовать скаляр, чтобы узнать что-то об угле между двумя векторами:

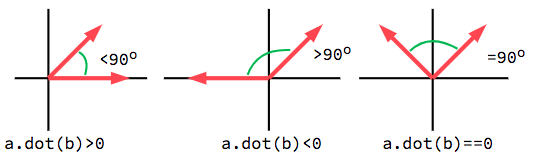
При использовании единичных векторов результат всегда будет находиться между значением -1 (180°) и 1 (0°).

Если два вектора указывают в одном направлении, то их скалярное произведение больше нуля. Когда они перпендикулярны друг другу, то скалярное произведение равно нулю. И когда они указывают в противоположных направлениях, их скалярное произведение меньше нуля - прим. автора

Угол обзора

Мы можем использовать эффект «угла обзора», чтобы определить, обращен ли объект лицом к другому объекту. На приведенном ниже рисунке игрок P пытается уйти от зомби A и B. Предположим, что угол обзора зомби 180°, могут ли они видеть игрока?

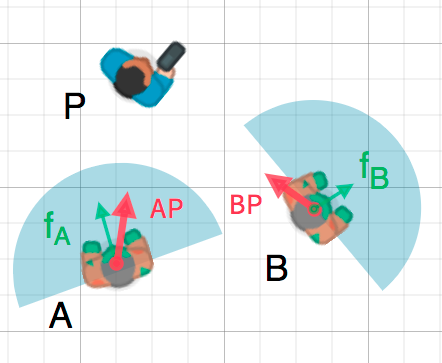
Зеленые стрелки fA и fB представляют собой единичные векторы, обозначающие направления движения зомби, а синий полукруг представляет собой поле зрения. Для зомби А находим вектор направления АР - используя действие Р-А находим вектор указывающий на игрока и далее нормализуем его. Если угол между найденным вектором и единичным вектором меньше 90°, тогда зомби заметит игрока.

В коде это будет выглядеть так:

var AP = (P - A).normalized()
if AP.dot(fA) > 0:
    print ("A sees P!")

Векторное произедение

Также как и скалярное произведение, векторное произведение это операция над двумя векторами. Хотя в результате векторного произведения вы получаете вектор с направлением перпендикулярным обоим, его длина зависит от их относительного угла. Если два вектора параллельны, в результате вы получите нулевой вектор.

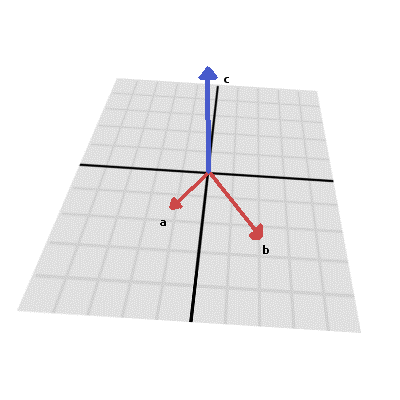
Векторное произведение выглядит следующим образом:

var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)

С помощью Godot вы можете использовать встроенный метод:

var c = a.cross(b)

В векторном произведении порядок имеет значение. a.cross(b) не даст того же результата, что и b.cross(a). Полученные векторы указывают на противоположные направления.

Расчет нормали

Одним из распространенных способов использования векторного произведения является расчет нормали к поверхности. Направления, в которых «смотрит» та или иная поверхность. Если у нас есть треугольник ABC, мы можем использовать векторное произведение для нахождения двух ребер AB (B - A) и AC (C - A). Используя векторное произведение AB x AC, находим вектор, перпендикулярный им обеим: т. е. перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».

Вот функция вычисления нормали треугольника:

func get_triangle_normal(a, b, c):
    # find the surface normal given 3 vertices
    var side1 = b - a
    var side2 = c - a
    var normal = side1.cross(side2)
    return normal

Ось вращения

В разделе «Скалярное произведение» мы увидели, как его можно использовать для определения угла между двумя векторами. Однако в 3D этой информации недостаточно. Нам также нужно знать, об оси вращения. Мы можем найти ее, применив векторное произведение текущего направления “взгляда” и направления цели. Полученный перпендикулярный вектор и будет является осью вращения.

http://docs.godotengine.org/en/3.0/tutorials/math/vector_math.html